MATLAB CODE FOR CIRCULAR CONVOLUTION

MATLAB CODE FOR CIRCULAR CONVOLUTION

The circular convolution, also known as cyclic convolution, of two aperiodic functions occurs when one of them is convolved in the normal way with a periodic summation of the other function.  That situation arises in the context of the Circular convolution theorem.  The identical operation can also be expressed in terms of the periodic summations of both functions, if the infinite integration interval is reduced to just one period.  That situation arises in the context of the discrete-time Fourier transform (DTFT) and is also called periodic convolution.  In particular, the transform (DTFT) of the product of two discrete sequences is the periodic convolution of the transforms of the individual sequences.

                                    

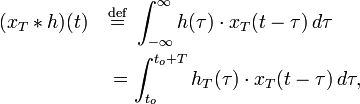
CODE:

clc;
disp('Input :');
x=input('Enter the first sequence : ');
h=input('Enter the second sequence : ');
N1=length(x);
N2=length(h);
N=8;
x=[x zeros(1,N‐N1)];
h=[h zeros(1,N‐N2)];
M=[0:1:N‐1];
disp(M);
h=h(M+1);
disp(h);
M=mod(‐M,N);
disp(M);
for n=1:1:N
            M=n‐1;
            p=0:1:N‐1;
            q=mod(p‐M,N);
            disp(q);
            hm=h(q+1);
            H(n,:)=hm;
            disp(H(n,:));
end
y=x*H;

%plot;
n1=0:1:N‐1;

subplot(3,1,1);
stem(n1,x);
title('First sequence');
xlabel('Sample...');
ylabel('Magnitude...');

subplot(3,1,2);
stem(n1,h);
title('Second sequence');
xlabel('Sample...');
ylabel('Magnitude...');

subplot(3,1,3);
stem(n1,y);
disp('The output is y= ');
disp(y);
title('Circular Convolution');
xlabel('Sample...');
ylabel('Magnitude…’);

OUTPUT:

        Enter the first sequence : [1 2 3 4]

        Enter the second sequence : [1 0 1 0 1]

        The output is y=

                 1 2 4 6 4 6 3 4